User Manual
Overview
Below are the ROS topics of each sensor modality in MCD. Please click on the link on each message type for their detailed definition. Other details such as resolutions are also provided. The naming convention `/<hardware-unit>/<modality>/…' is applied for all topics in both the ATV and HHS setups. Note that the ‘t' and ‘b' affixes in the names of the realsense D455 modules refer to ‘top' and ‘bottom' units. They do not mean a hardware variant.
| Modality | Hardware | ROS topics / Sensor suite | Message type | Rate (Hz) | Notes | |
|---|---|---|---|---|---|---|
| ATV | HHS | |||||
| Camera | D435i | /d435i/infra1/image_rect_raw /d435i/infra2/image_rect_raw | - | sensor_msgs/Image | 30 | 640×480 Greyscale 640×480 Greyscale |
| D455t | - | /d455t/infra1/image_rect_raw /d455t/infra2/image_rect_raw /d455t/color/image_raw | 30 | 640×480 Greyscale 640×480 Greyscale 640×480 RGB | ||
| D455b | /d455b/infra1/image_rect_raw /d455b/infra2/image_rect_raw /d455b/color/image_raw | /d455b/infra1/image_rect_raw /d455b/infra2/image_rect_raw /d455b/color/image_raw | 30 | 640×480 Greyscale 640×480 Greyscale 640×480 RGB | ||
| IMU | Ouster OS1 | /os cloud node/imu | /os cloud node/imu | sensor_msgs/Imu | 100 | IAM-20680HT |
| D435i | /d435i/imu | - | 400 | Bosch BMI055 | ||
| D455t | - | /d455t/imu | 400 | See datasheet | ||
| D455b | /d455b/imu | /d455b/imu | 400 | See datasheet | ||
| VN100 | /vn100/imu | - | 400 | 9-axis IMU (datasheet) | ||
| VN200 | /vn200/imu | /vn200/imu | 400 | 9-axis IMU (datasheet) | ||
| Lidar | Ouster OS1 | /os cloud node/points | /os cloud node/points | sensor_msgs/PointCloud2 | 10 | 128 channel for ATV, 64 channel for HHS Points per channel: 1024 Point format: see our manual |
| Livox Mid70 | /livox/lidar | /livox/lidar | livox_ros_driver/CustomMsg | 10 | 1 channel. Points per channel: 9984 Point format: see our manual | |
| UWB | Link Track P | /ltp tag0/nlnf3 /ltp tag1/nlnf3 | /ltp tag0/nlnf3 /ltp tag1/nlnf3 | nlink_parser/LinktrackNodeframe3 | 20 | See datasheet |
| GPS | VN200 | /vn200/GPS | - | sensor_msgs/NavSatFix | 400 | See datasheet |
Lidar data
Resolution and rate
For the ntu_ sequences, the ouster lidar has 128 channels with 1024 points per channel. For the kth_ and tuhh_ sequences, the ouster lidar has 64 channels with 1024 points per channel. In all sequences, the mid70 Livox lidar have one single non-repetitive line with 9984 points per line. All lidars output data at 10 Hz.
Point format
For ouster lidar, the C++ definition of the point struct by the PCL convention is as follows:
struct PointOuster
{
PCL_ADD_POINT4D;
float intensity;
uint32_t t;
uint16_t reflectivity;
uint16_t ambient;
uint32_t range;
uint8_t ring;
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
} EIGEN_ALIGN16;
POINT_CLOUD_REGISTER_POINT_STRUCT(PointOuster,
(float, x, x) (float, y, y) (float, z, z)
(float, intensity, intensity)
(uint32_t, t, t)
(uint16_t, reflectivity, reflectivity)
(uint16_t, ambient, ambient)
(uint32_t, range, range)
(uint8_t, ring, ring)
)
For python programming, we recommend using the pypcd package, which can read the pointcloud directly from ROS message into structured numpy array with the field names intact. Please find the demo here.
For livox lidar, the point has a custom structure that is defined by the manufacturer as follows:
# Livox costum pointcloud format.
uint32 offset_time # offset time relative to the base time
float32 x # X axis, unit:m
float32 y # Y axis, unit:m
float32 z # Z axis, unit:m
uint8 reflectivity # reflectivity, 0~255
uint8 tag # livox tag
uint8 line # laser number in lidar
Please follows the instructions here to install the livox driver, after which you should be able to import and manipulate the livox message in ROS python or C++ program.
Time stamp
For MCD, please take note of the following:
- For the ouster data, the timestamp in the message header corresponds to the end of the 0.1s sweep. Let us denote it as \(t_h\). Each lidar point has a timestamp (in nanosecond) that is relative to the start of the sweep, denoted as \(t_r\). The absolute time of the point \(t_a\) is therefore:
- For the livox data, the timestamp in the message header corresponds to the start of the 0.1s sweep. We us denote it as \(t_h\). Each lidar point has a timestamp (in nanosecond) that is relative to the start of the sweep, denoted asc \(t_r\). The absolute time of the point \(t_a\) is therefore:
Coordinate systems
The main coordinate systems in MCD is defined as follows:
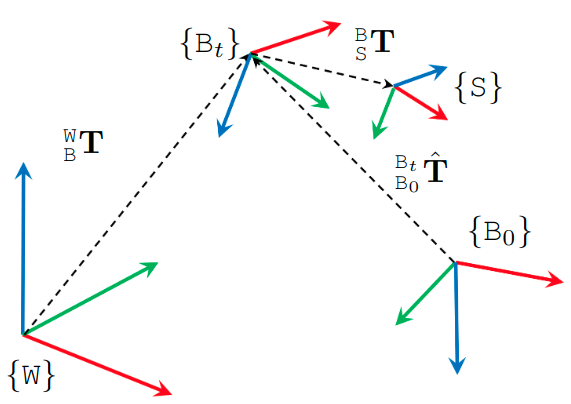
First, the coordinate system of the prior maps is referred to as the World frame \(\mathtt{W}\). Then the Body frame \(\mathtt{B}\) coincides with the VN100 IMU in the NTU sequences, and the VN200 in the KTH and TUHH sequences. Each sensor has a Sensor frame \({\mathtt{S}}\) attached to it.
The extrinsics of the sensors in MCD are declared as transformation matrices \({}^{\mathtt{B}}_{\mathtt{S}}\bf{T} = \begin{bmatrix} {}^{\mathtt{B}}_{\mathtt{S}}\mathrm{R} & {}^{\mathtt{B}}_{\mathtt{S}}\mathrm{t} \\ 0 &1\end{bmatrix}\), where \({}^{\mathtt{B}}_{\mathtt{S}}\mathrm{R}\) and \({}^{\mathtt{B}}_{\mathtt{S}}\mathrm{t}\) are respectively the rotational and translational extrinsics.
Therefore if one observes a landmark \({}^{\mathtt{C}}\mathrm{f}\) in the camera frame \(\mathtt{C}\), its coordinate in the body frame \({}^{\mathtt{B}}\mathrm{f}\) is calculated as:
\[{}^{\mathtt{B}}\mathrm{f} = {}^{\mathtt{B}}_{\mathtt{C}}\mathrm{R} {}^{\mathtt{C}}\mathrm{f} + {}^{\mathtt{B}}_{\mathtt{C}}\mathrm{t}\]The ground truth data in our csv files are the poses \(({}^{\mathtt{W}}_{\mathtt{B}_t}\mathrm{q}, {}^{\mathtt{W}}_{\mathtt{B}_t}\mathrm{p})\), where \({}^{\mathtt{W}}_{\mathtt{B}_t}\mathrm{q}\) and \({}^{\mathtt{W}}_{\mathtt{B}_t}\mathrm{p}\) are the orientation (in quaternion) and position of the body frame at time t relative to the world frame.
In most cases, the SLAM estimate \({}^{\mathtt{B}_0}_{\mathtt{B}_t}\hat{\bf{T}}\) is relative to the coordinate frame that coincides with the body frame at initial time. It is therefore neccessary to align the SLAM estimate with the groundtruth. The evo package is a popular tool for this task.